Identidade de Euler
A Matemática, às vezes, pode parecer difícil, complicada, até mesmo fora da realidade. Mas também pode ser instigante e bela. Para nós que gostamos da Matemática, nem pensamos nisso, pois já faz parte de nossas vidas.
Uma Identidade Matemática
é uma igualdade que permanece verdadeira para quaisquer que sejam os valores
das variáveis que nela apareçam, diferentemente de uma Igualdade Matemática que
pode ser verdadeira somente sob condições particulares.
A Identidade de Euler
reúne talvez os cinco números mais importantes da Matemática (0, 1, i, e, π) em uma simples igualdade:
Para verificar esta
igualdade, vamos fazer a demonstração da Identidade de Euler. Para isso, vamos
considerar o exponencial ex em sua forma de série infinita:

Usamos aqui um artifício
que será muito útil para a dedução da identidade. Fazemos:
E substituímos em (1):
Do estudo dos Números
Complexos, sabemos que:

Substituímos (4) em (3), encontrando

e
Substituímos (6) e (7) na relação (5), obtendo:
Agora, se fizermos z
= π, teremos:
No entanto, a
trigonometria nos garante que:
e
Substituindo estes
valores na relação (9), chegaremos a:






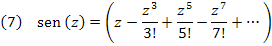


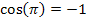



Nenhum comentário:
Postar um comentário