Sobre o autor
domingo, 26 de junho de 2016
Grandes Cientistas: Srinivasa Ramanujan
Grandes Cientistas: Srinivasa
Ramanujan
-Hardy,
qual o número do taxi que você veio?
-Um
número sem importância, sem relevância, era o 1729.
-Não
Hardy, esse é um belo número. Ele é o menor inteiro formado pela soma de dois
outros inteiros elevados ao cubo!
Essa conversa se
passou no leito de um hospital em Londres, por volta de 1920, quando o
matemático indiano Srinivasa
Ramanujan tratava de tuberculose. G.H. Hardy era um dos mais
proeminentes e famosos matemáticos da Inglaterra, estudioso na área de Teoria
dos Números. A história de Ramanujan, hoje semideus e herói nacional da India,
é uma história triste, melancólica e que merecia um final feliz para ele.
Nascido num
vilarejo pobre da India, Ramanujan só teve um livro na vida. Era um livro de
matemática que ele levava para todo lugar, com mais de 6.000 fórmulas agrupadas
como um guia de álgebra. Suas irmãs contaram que ele largou as brincadeiras
ainda com 9 anos para ficar o dia todo fazendo contas e mais contas em seus
cadernos. Nem mesmo ir a escola ele quis, desistindo do ensino médio. Graças a
ajuda de amigos, conseguiu um emprego num porto, como cobrador de impostos
local no porto de Madrasta.
Mas nas horas
livres, escrevia fórmulas e milhares de números em seus cadernos. Um certo dia,
descobriu o nome de três grandes matemáticos da Inglaterra. Enviou uma carta
para cada um, com a descrição sobre sua demonstração de 120 teoremas. Dois dos
matemáticos nem leram a carta e jogaram-na no lixo, pensando se tratar de algo
fraudulento ou coisa de louco.
O terceiro
matemático era G.H.Hardy,
idolatrado por Ramanujan, mas que também jogou sua carta no lixo. No entanto,
ao receber a visita de outro amigo matemático, Hardy comentou sobre a tal carta
de um indiano. O amigo John
Littlewood se assustou com o que viu, e alertou a Hardy que ali
estavam provas de diversos teoremas que muitos estavam atrás. Não era uma
fraude, era uma preciosidade. Ambos passaram a noite inteira lendo e revisando
os resultados e se maravilharam com aquilo.
Alguns meses
depois, Hardy conseguiu que Ramanujan fosse para Londres, custeado com uma
bolsa de Cambridge. Segundo Hardy contou sobre o fato, foram os cinco anos de
maior progresso na história da Teoria dos Números. Ramanujan aparecia todos os
dias com páginas contendo de 5 a 10 resultados novos na sala de Hardy. No total
de sua vida, Ramanujan produziu cerca de 4900 páginas de resultados e centenas
de teoremas, a maioria ainda sem prova.
Mas a
permanência de Ramanujan em Londres lhe causou a morte. Acostumado a pouca
comida e alimentos tendo como base os vegetais, Ramanujan vivia doente por
causa das refeições. Em cinco anos adquiriu uma tuberculose, e voltou para a
India, onde morreu pobre. Em 1976 George Andrews descobriu na biblioteca de
Cambridge o que hoje é chamado de "o livro perdido de Ramanujan". O
mundo ficou ainda mais atônito com as anotações esquecidas dentro da biblioteca
pelo próprio Ramanujan.
Com sua morte,
terminava para Ramanujan a trajetória do cometa mais rápido e brilhante da
India e da Teoria dos Números. Sobre o número 1729 ao qual se referiu
Ramanujan, o que ele disse para Hardy em seu leito no hospital era matematicamente
o que aparece à seguir.
Não existe outro
número menor do que 1729 que pode ser formado pela soma dos cubos de dois
inteiros. Mas não é só isso. Depois de sua morte, descobriu-se um baú inteiro
de fórmulas as quais Ramanujan descobriu ou reinventou sozinho em sua casa na
India. Os especialistas em Teoria dos Números dizem que foi lamentável alguém
como Hardy ficar muito tempo sozinho. Mais da metade da sua vida ele passou
descobrindo métodos que já existiam. Sozinho ele redescobriu sem informação de
ninguém 100 anos de teoria matemática.
Por exemplo,
Ramanujan tinha uma enorme facilidade em tratar com o infinito. Segundo suas
próprias palavras, ele dormia e sonhava com a deusa hindu Namagiri. Era ela
quem lhe contava sobre os teoremas e sobre as demonstrações em seus sonhos. Eis
uma de suas resoluções interessantes sobre o número 3.
Outra
contribuição até hoje esplêndida é sobre a partição de um número. Por exemplo,
de quantas maneiras você pode escrever um número? Seja o número N = 4.
Esse número pode
ser:
4
3+1
2+2
2+1+1
1+1+1+1
Mas Ramanujan
criou uma fórmula "mágica", testada em computadores com mais de 100
dígitos que possui erro mínimo. A fórmula está ao lado, e ninguém tem a menor
noção sobre como ele, apenas manipulando números chegou de forma brilhante
nela.
A fórmula das
partições é famosa e leva o nome do mentor de Ramanujan, o matemático que lhe
acolheu G.H.Hardy e Ramanujan aparece em segundo lugar.
Ele também criou
fórmulas para o número irracional Pi, para o inverso ao quadrado de Pi, para
raízes com somas infinitas e desenvolveu a mais controvérsia de suas fórmulas.
Todos sabem que
somando-se os inteiros a partir do número 1, infinitamente, o resultado é
infinito. Essa é conhecida como uma série divergente, pois nunca estaciona em
nenhum número finito.
Não é bem isso
que Ramanujan provou. A prova dessa soma infinita dá exatos -1/12. Sim, um
número racional, negativo e... finito! Como?
Uma prova bem
engraçada pode ser acompanhada com o pessoal do Numberphile,
vale à pena, é bem simples e didática para todo mundo.
Mas o mais
interessante de tudo, antes que qualquer um fique achando que é uma bobagem,
apenas uma brincadeira matemática, é que essa descoberta de Ramanujan tem
aplicação física. E foi uma salvação para a explicação de um fenômeno na física
quântica.
Em 1948 o físico
Hendrick Casimir dos laboratórios da Philips previu que duas placas metálicas
perfeitamente paralelas num vácuo pefeito, e estando ambas descarregas, estão
sujeitas a se atrair.
A força somente
seria observada e mensurável a distância da ordem de diâmetros de átomos, na
casa dos microns. Mesmo estando em vácuo perfeito, o vácuo possui flutuações
causadas por partículas de fótons que se aniquilam e se recriam o tempo todo.
Ou seja, seria formado por antipartículas e partículas, numa luta de uma contra
outra para sobreviver.
Estando as
placas paralelas e no vácuo, a distâncias muito pequenas, com poucas partículas
internas, ao se aniquilarem o fluxo de energia se torna negativo entre essas
placas. E isso faria as placas se atraírem.
Bobagem teórica?
Pois esse efeito
foi observado em 1997 por Steve Lamoreaux de Los Alamos (EUA), depois em 2002 e
por fim em 2008, onde foi observada no laboratório a levitação quântica,
conforme prevista por Casimir.
A fórmula final
para a soma das infinitas frequências dos fótons em forma de onda que se criam
e se aniquilam é 1+2+3+...= -1/12. Sim, a soma infinita das frequências é
representada por uma variação negativa no fluxo de energia.
Isso mostra que
Ramanujan, com suas fórmulas e brincadeiras sobre números, conseguiu ajudar a
compreensão de um fenômeno observado 80 anos depois de sua morte. Graças a
Ramanujan os físicos conseguem calcular o raio de aproximação ideal das placas,
para que o fenômeno possa ser observado.
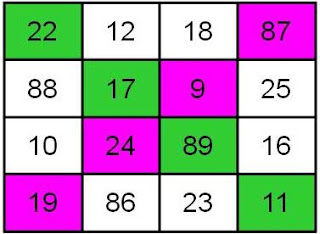
E por fim,
Ramanujan criou seu quadrado mágico.
O que tem de
especial? A soma das linhas sempre fornece resultado final 139. Por exemplo,
22+12+18+87 = 139. As colunas também, quando somadas fornecem 139. E as
diagonais? Sim, são 139. Mas o mais interessante é a primeira linha. Os números
22, 12, 18, 87 são na verdade a data de nascimento de Ramanujan: 22-12-1887.
Ramanujan criou
seu quadrado mágico partindo da data de seu nascimento para nunca ficar
esquecido. Nem precisava, pois com sua contribuição gigantesca os matemáticos
modernos ainda vão levar mais de dois séculos para provar seus teoremas.
facebook.com/matematica314
Assinar:
Postar comentários
(Atom)
0 comentários:
Postar um comentário